QSN - 3D Printer Torture Test Art (Quasicrystalline Spin Network)

QSN - 3D Printer Torture Test Art (Quasicrystalline Spin Network)
Published 2017-05-19T17:06:58+00:00
This is the QSN (Quasicrystalline Spin Network.)
First and foremost, Please watch the video attached so you have most of the information you need to print this. :
Second, This is my challenge to the 3D printing community, Can you Print it?
I spent over 3 months trying to get this to print extremely well. It took all kinds tweaks and Tests, BUT the very first one I tried WORKED! So i know you can do it too. after you get one printed, its all tweaking from there! How much better can you make it? I have about 30 of them Printed now. each with a new tweak!
My coworker Ray had this pulled up on his screen when I went into his office and I said, "I think I can print that"... and 3 months later here we are!
I spent way to much time trying to tune my built from scratch Restock delta to make perfect prints of the QSN. I eventually achieved this goal. Now I can print some really amazing prints of the QSN.
This is no easy print, however, I really would LOVE feed back from others who try to print one. I'm interested in seeing your method of printing this. Things such as:
How did you generate support?
What printer you are using?
What filaments did you try?
What slicers did you get to work?
Were you able to generate a solid?
Anything else you think would be helpful to share!
I have had almost No luck making this a solid. It's currently "stick and balls". You will need to make sure your slicer can handle that. I did get Meshmixer to make it a water tight solid, but it has to many triangles. Its almost overloaded for most average computers. You need a lot of ram.
So if you try this, use the stick and balls version, and make sure your slicer can handle it.
If you have any luck making this a solid please let me know.
Something I did not mention in the video was that I did try to build custom supports in Meshmixer as well as PreForm, but it was not achievable. Please give it a go and let me know if you get custom supports to work.
Challenge excepted ? :)
I'm not giving out my slicer settings just yet, because I'm interested in how you get it to work best! Later I will publish my Slicer settings that I have. However, in reality each system will be different any how and require your own settings...
You can find more of my 3D printing research here:
http://rwgresearch.com/open-projects/3d-printing-research/
Much Love & God Bless,
~Russ Gries
My YouTube(s)...
Main Content:
https://www.youtube.com/user/rwg42985
Live 3D printing & Stuff...
https://www.youtube.com/channel/UC0JRhK5DUp4Mr_WgNBnV57A
Print Settings
Printer:
Custom Rostock (Built in 2012)
Resolution:
.175mm-.2mm for big models
Infill:
no
Notes:
only use raft if you dont get good bed adhesion. use 1 layer and less Than 50% infill. works for me...
How I Designed This
Ray Did The Math, Russ Did Some Small changes...
We build the QSN by taking a cuboctahedron, an Archimedean solid made of 8 triangular faces and 6 square faces, and 12 vertices, and keep only 4 triangular faces, not touching one another, built on the 12 vertices.
We link these 4 triangles to the center and get 4 tetrahedra sharing a vertex in the center, the basis of a FCC lattice.
We translate each tetrahedron along an edge bringing the center to an external vertex, and repeat the operation, getting an FCC lattice.
Then, we “Fibonacci-space” this lattice, by inserting gaps of the edge size divided by the golden ratio, such that each ray emanating from the center becomes a Fibonacci chain. We get a Fibonacci-spaced FCC lattice.
Then we duplicate this lattice 4 more times, to finally get 5 copies; and we rotate four of the five copies, such that the 20 tetrahedra sharing the center aligns all their faces in only 10 planes.
There is two ways to get there, and the object made of the 20 tetrahedra in the center becomes a 20-group, a geometric figure discovered by our team some years ago.
The two ways assign a chirality to the object, and to the compound of the 5 Fibonacci-spaced FCC lattices. We choose one of the two possible chiralities.
We have later found that the 60 vertices of the 20 central tetrahedra are the vertices of the regular compound of 5 cuboctahedra (https://en.wikipedia.org/wiki/Compound_of_five_cuboctahedra )
And more recently we have found that the cuboctahedron is the Dirichlet sphere of radius square root of 2, while the 20-group is the next Dirichlet sphere of radius square root of 8, where we have defined the Dirichlet spheres as the spheres whose 3D radius is equal to the 6D radius, if x,y,z are Dirichlet integers of the form a+b phi (a, b integer and phi the golden ratio), and restrict to regular tetrahedra made of one equilateral triangle on the sphere and the fourth vertex at the center, which explain their non-arbitrary algebraic emergence.
Now that we have this superposition of 5 differently oriented Fibonacci-spaced FCC, otherwise seen as a bunch of regular tetrahedra, which we name our possibility space, we select only from the available vertices, the ones which are themselves centers of 20-groups: they become a set of vertices.
We automatically select all the pairs of this vertices which are at two possible distances, one being golden ratio times the other. These edges are what is 3D printed.
We check that they are organized as a set of dodecahedra, and two sets of icosahedra, the larger edge to the smaller being the golden ratio.
You can search and find this dodecahedra and icosahedra in the QSN.
Because of the limited combinatoric ways of connecting this edges and the fact that all the space is covered, this is a 3D quasicrystal.
Our team has also published many relationships between this quasicrystal and the Elser-Sloane quasicrystal obtained by projecting the E8 lattice, which links it to particle physics.
~Raymond Aschheim
For more read this paper:
https://arxiv.org/pdf/1511.07786.pdf
Deeper Look At What The QSN is.
The QSN or Quasicrystalline Spin Network is a 3D representation of a 4D quasicrystal, called the Elser-Sloane Quasicrystal, which is created by projecting the E8 lattice to 4D. This 4D quasicrystal is made entirely of regular, 3D tetrahedra, which is achieved due to the particular angle of the E8 to 4D projection. When we take any five, 3D subspaces of this 4D quasicrystal (one subspace being all tetrahedra that are oriented in the same direction) and then rotate them from one another by 15.552* degrees, we come up with a 3D quasicrystal that can be seen as a representation of the 4D, Elser-Sloane quasicrystal. We call this new, 3D quasicrystal the “compound quasicrystal.” Why is the compound quasicrystal important? It is important because of its relationship to the QSN.
The QSN is the densest possible 3D network of point-sharing Fibonacci chains and is the most computationally efficient point space in 3D. It is created by taking the FCC lattice (a point space that provides the densest packing of 3D spheres) and then spreading its points until they are spaced according to the Fibonacci sequence. We then take this new lattice of Fibonacci spaced points, clone it five times and rotate the five clones from one another by 15.522 degrees to create the QSN.
As it turns out, the compound quasicrystal is an exact subspace of the QSN: the QSN contains all legal configurations of the Elser-Sloane, E8-to-4D quasicrystal.
The QSN therefore is deeply related to the E8 lattice and its 4D projection.
http://www.quantumgravityresearch.org/portfolio/the-quasicrystalline-spin-network-2
Disclaimer
YOU are responsible for any damage caused by attempting to 3D Print these files! Always keep an eye on your 3D Printers when attempting challenging prints.
Extras:
a more fun video of the QSN
first " clean" print
live print of the very first try!
lights and sounds af a MICRO QSN
This Was Awesome. Angus & Joel's Reaction to the QSN In Person.
25MM QSN With .4mm Nozle & Quick Look At My Hotend / Extruder ( In 4K)
| Date published | 19/05/2017 |
| Technologie | FDM |
| Schwierigkeitsgrad | Very Difficult |










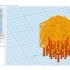























wonderful model, print simply with an Elegoo Mars 2 and standard resin Elegoo red, no postprocessing.